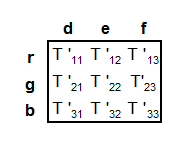Doug Kerr
Well-known member
I will discuss in this series of notes some conundrums in the "color response" page of the DxOMark reports on camera sensor characteristics. In this first note, I will discuss some background matters.
The sRGB primaries
All "RGB family" color spaces are tristimulus color spaces (although many purists reserve that term for a particular color space of that class, the CIE XYZ color space). That means that the color of an instance of light is described by stating the amounts of three defined kinds of light, called the "primaries" of the color space, which,. if combined, would create light of the color of interest.
In the case of color spaces of the RGB family, including the specifically defined color space identified as sRGB", those three primaries are called R, G, and B.
Thus three primaries are defined in terms of their chromaticities and base luminances, given in terms of the CIE x ,y, Y color space.
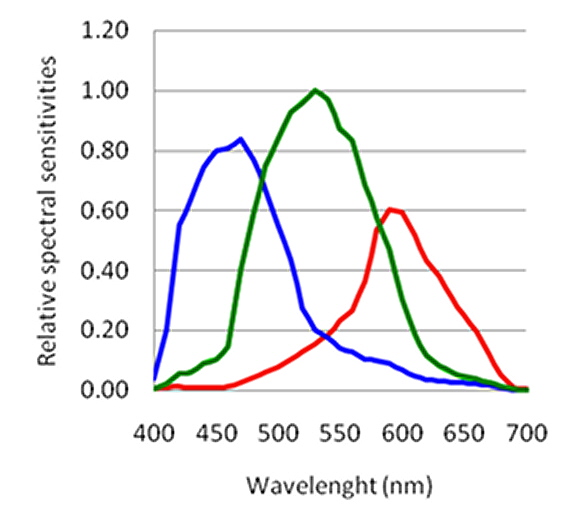
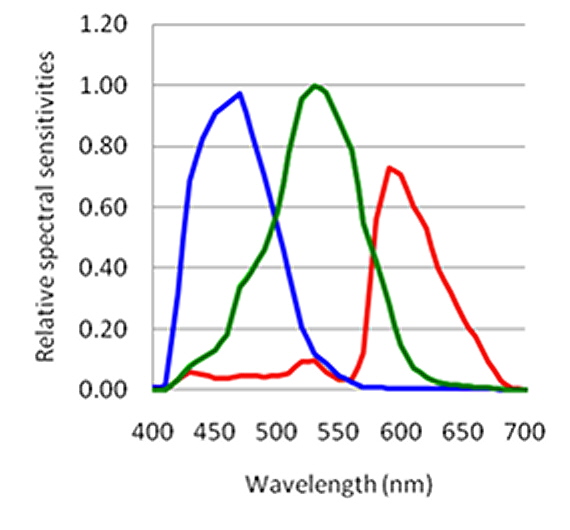
Now we know that, for any given color of light, there are an infinite number of kinds of light, with different spectrums, that have that color. (Some wouild suggest that I say, "appear to the eye to have that color", but in fact the definition of color is such that if two instances of light "appear to the eye to have the same color", they are the same color.) This is the phenomenon of metamerism.
Now we might be tempted to ask, "Does not the complete definition of the three RGB primaries include a standard spectrum for each"? No, it does not. There is no need to do do.
The reason is that if we take two instances of light, both of known color (that is, known chromaticity and known luminance) and combine them, then the resulting light will have a predictable color. This is independent of how those two instances got their colors (what spectrums they had). Thus, we need not think in terms., for the definitions of the sRGB primaries, of anything beyond their colors (most important to us is the matter of their chromaticities.
Suppose that for some kind of test we wanted to make of a camera sensor, we wanted a machine that would emit, on command, "the sRGB primaries". Just what would that mean? Would we care what spectrums these three outputs had? The sensor response might depend on that (see below).
We can see that the notion of such a machine is very problematical.
Sensor behavior
It would be very desirable if, in our sensors:
But, certainly in all the cases I have heard of, that is not so.
We realize that (as mentioned above) there are an infinity of light spectrums that all have the same color (remembering that "color" is in fact defined in terms of the human response to the light of interest). This is the phenomenon of metamerism,
If in fact attribute A were true for our sensor (such a sensor is called colorimetric, meaning, "measures color), then for light of any spectrum having a certain color, the sensor d, e, and f outputs would be the same (and would tell us, consistently, the color of that light).
But, for the typical sensor, if we apply two instances of light having different spectrums but the same color (these would be called metamers), the sensor would in general deliver different sets of d, e, and f values. This is a shortcoming we can't overcome, but can "dodge" (more about that later).
Now if we had a sensor that did exhibit attribute A, it might be very handy if, in addition:
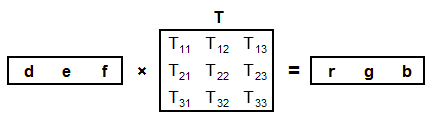
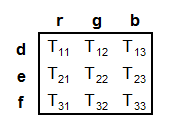
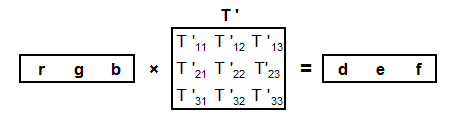
Then, after demosaicing (so we had a d, e, and f value for each pixel location), we could just take the d, e, and f values for any pixel and (perhaps after scaling) proceed directly to convert them (by applying "gamma precompensation") to the R, G, and B values (sRGB basis) of the pixel in the developed image.
Of course, since, for our sensors, attribute A does not obtain, then attribute B is moot. But the notion will play a role in what is to follow.
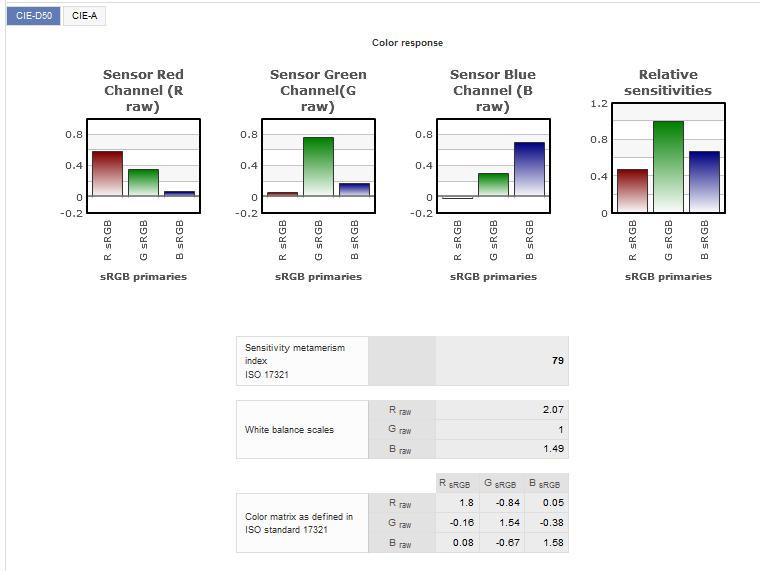
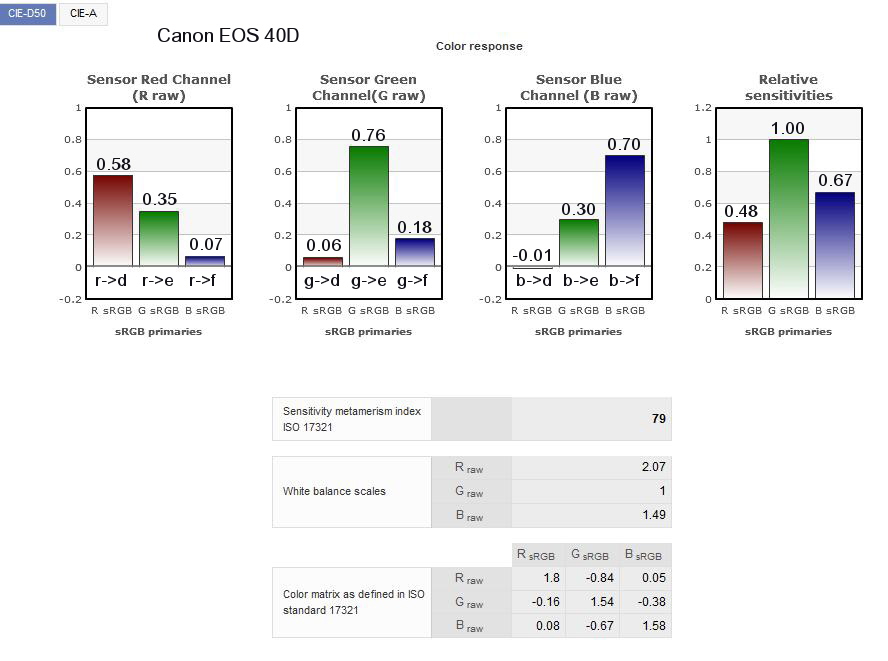
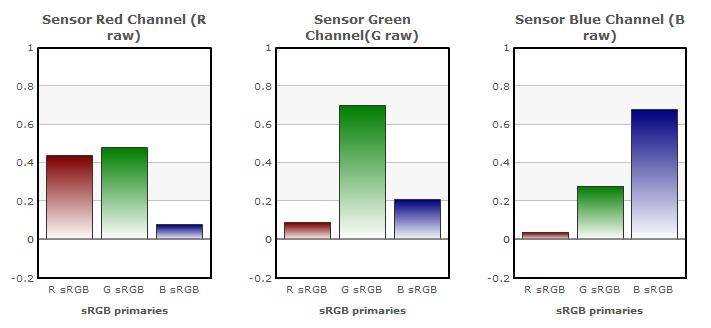
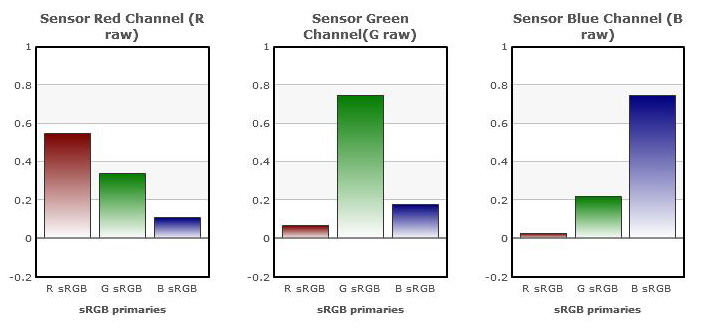
To slightly circle back to a point made in the previous section, suppose that for some reason, as part of a series of tests to investigate the behavior of a certain sensor, we decided to measure its outputs (d, e, and f values) when it was stimulated (separately), by "the three sRGB primaries". This at first sounds like it could be useful, and the results very informative.
But now we have to think more about just what that would mean. What kinds of light might we use as "the three sRGB primaries? What spectrums would they have (remembering that the primaries are only defined in terms of their colors, and there are an infinity of spectrums that would have a each of those colors)?
Maybe that wouldn't matter. Well, that wouild be true if the sensor were colorimetric (that is, if its d, e, and f outputs depended only on the color of the light, regardless of the spectrum that give it that color).
But we have just seen that for actual sensors the d,,e, and f outputs do not depend on the color of the light, independent of the spectrum that gave it that color.
So if we are going to test the response of the sensor when it is excited by "one of the sRGB primaries", what spectrums would we prescribe for the three "test lights"? And why those particular ones.
So maybe "testing the response of a sensor to excitation by 'the sRGB primaries' " is not actually a good idea.
Hold that thought.
[to be continued]
Best regards,
Doug
The sRGB primaries
All "RGB family" color spaces are tristimulus color spaces (although many purists reserve that term for a particular color space of that class, the CIE XYZ color space). That means that the color of an instance of light is described by stating the amounts of three defined kinds of light, called the "primaries" of the color space, which,. if combined, would create light of the color of interest.
In the case of color spaces of the RGB family, including the specifically defined color space identified as sRGB", those three primaries are called R, G, and B.
Thus three primaries are defined in terms of their chromaticities and base luminances, given in terms of the CIE x ,y, Y color space.
Now we know that, for any given color of light, there are an infinite number of kinds of light, with different spectrums, that have that color. (Some wouild suggest that I say, "appear to the eye to have that color", but in fact the definition of color is such that if two instances of light "appear to the eye to have the same color", they are the same color.) This is the phenomenon of metamerism.
Now we might be tempted to ask, "Does not the complete definition of the three RGB primaries include a standard spectrum for each"? No, it does not. There is no need to do do.
The reason is that if we take two instances of light, both of known color (that is, known chromaticity and known luminance) and combine them, then the resulting light will have a predictable color. This is independent of how those two instances got their colors (what spectrums they had). Thus, we need not think in terms., for the definitions of the sRGB primaries, of anything beyond their colors (most important to us is the matter of their chromaticities.
Suppose that for some kind of test we wanted to make of a camera sensor, we wanted a machine that would emit, on command, "the sRGB primaries". Just what would that mean? Would we care what spectrums these three outputs had? The sensor response might depend on that (see below).
We can see that the notion of such a machine is very problematical.
Sensor behavior
It would be very desirable if, in our sensors:
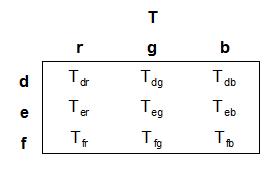
A. the three outputs (which I call d, e, and f to avoid misunderstandings) actually described the color of the light hitting the sensor.
But, certainly in all the cases I have heard of, that is not so.
We realize that (as mentioned above) there are an infinity of light spectrums that all have the same color (remembering that "color" is in fact defined in terms of the human response to the light of interest). This is the phenomenon of metamerism,
If in fact attribute A were true for our sensor (such a sensor is called colorimetric, meaning, "measures color), then for light of any spectrum having a certain color, the sensor d, e, and f outputs would be the same (and would tell us, consistently, the color of that light).
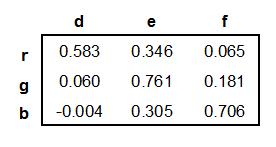
But, for the typical sensor, if we apply two instances of light having different spectrums but the same color (these would be called metamers), the sensor would in general deliver different sets of d, e, and f values. This is a shortcoming we can't overcome, but can "dodge" (more about that later).
Now if we had a sensor that did exhibit attribute A, it might be very handy if, in addition:
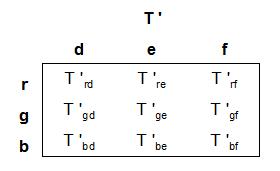
B. the sensor outputs, d, e, and f, would (perhaps after applying some fixed scaling to compensate for their differing "sensitivities") corresponded to the linear coordinates of the color space in which we intended to work. Perhaps they would correspond to the linear coordinates, r,. g, and b, of the sRGB color space.
Then, after demosaicing (so we had a d, e, and f value for each pixel location), we could just take the d, e, and f values for any pixel and (perhaps after scaling) proceed directly to convert them (by applying "gamma precompensation") to the R, G, and B values (sRGB basis) of the pixel in the developed image.
Of course, since, for our sensors, attribute A does not obtain, then attribute B is moot. But the notion will play a role in what is to follow.
To slightly circle back to a point made in the previous section, suppose that for some reason, as part of a series of tests to investigate the behavior of a certain sensor, we decided to measure its outputs (d, e, and f values) when it was stimulated (separately), by "the three sRGB primaries". This at first sounds like it could be useful, and the results very informative.
But now we have to think more about just what that would mean. What kinds of light might we use as "the three sRGB primaries? What spectrums would they have (remembering that the primaries are only defined in terms of their colors, and there are an infinity of spectrums that would have a each of those colors)?
Maybe that wouldn't matter. Well, that wouild be true if the sensor were colorimetric (that is, if its d, e, and f outputs depended only on the color of the light, regardless of the spectrum that give it that color).
But we have just seen that for actual sensors the d,,e, and f outputs do not depend on the color of the light, independent of the spectrum that gave it that color.
So if we are going to test the response of the sensor when it is excited by "one of the sRGB primaries", what spectrums would we prescribe for the three "test lights"? And why those particular ones.
So maybe "testing the response of a sensor to excitation by 'the sRGB primaries' " is not actually a good idea.
Hold that thought.
[to be continued]
Best regards,
Doug