Doug Kerr
Well-known member
There have been several recent discussions here one aspect of which is essentially "what is the largest f-number we can use without the effect of diffraction in diminishing the system resolution becoming 'unacceptable'."
This discussion is gravely hampered by the facts that:
• There is no actual analytical definition of the "resolution" of a system.
• There is no obvious criterion of how much diminution of this elusive property is "unacceptable".
But let's see what we do know about the relationships involved.
The phenomenon of diffraction means that, assuming a perfect lens, a point on the object will be imaged not as a point but as a finite-sized "diffraction figure", which for a circular aperture with "knife edges" will have the illuminance pattern we call the "Airy figure". We can characterize this analytically as a "point spread function".
This spreading results in a decrease in the "response" of the system (a declining MTF) as the spatial frequency increases.
For any given point spread function, there is a unique MTF curve, which can be rigorously calculated by straightforward mathematics.
In the case of our ideal circular aperture, that MTF curve is as shown by the solid line on this figure:
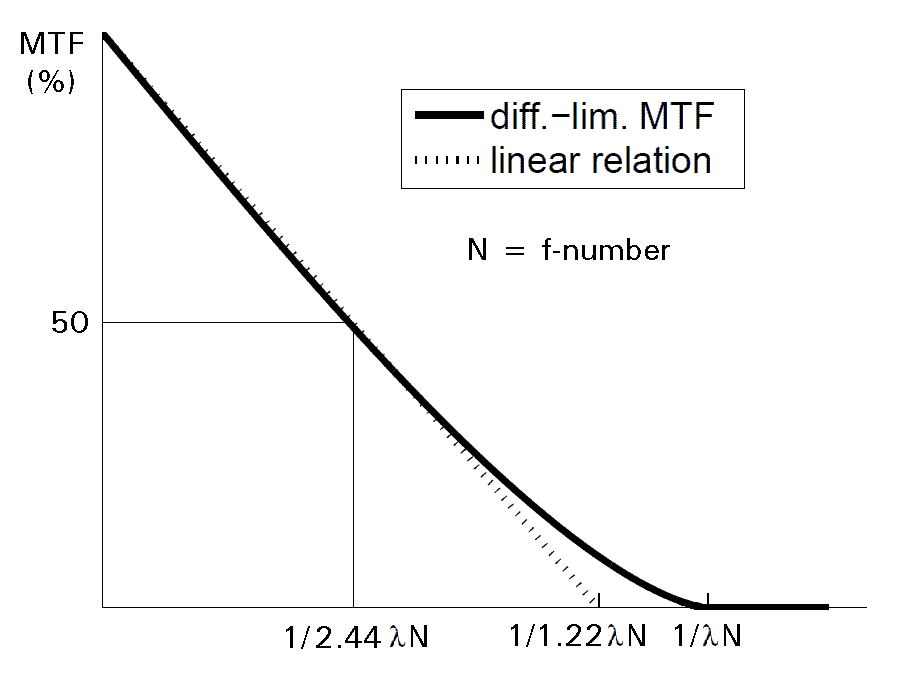
Recall that the MTF of the system is the MTF of the lens and the sensor multiplied (at each spatial frequency) by this MTF.
We often choose to say, quite arbitrarily, that the resultion of the entire system is the spatial frequency where the system MTF is 50%. Perhaps it is reasonable to say, equally arbitrarily, that the impact of diffraction on the resolution is "significant" at the spatial frequency where the diffraction MTF is 50%.
We see this on the chart as a spatial frequency of 1/2.44LN.
Let's say that we choose an f-number such that the zero of the straight line approximation of the diffraction MTF is at the Nyquist frequency of the sensor. Recall that this is an absolute limit on the spatial frequency that can be captured by the system (even with a "perfect" lens and negligible diffraction effect). That is, we have arranged for the response due to diffraction (in its straight line approximation) to just "poop out" at the Nyquist frequency, at or above which the sensor could not possible respond anyway.
The Nyquist frequency is defined as 1/2p, where p is the sensel pitch of the sensor. (We will assume a monochrome sensor to avert the need to deal with the complications of a CFA sensor, and assume a wavelength of 555 nm, as is common in this matter.)
After a little algebra, we find that in the situation where the diffraction MTF is 50%, the diameter of the Airy circle is twice the pixel pitch (or, the pixel pitch is the radius of the Airy disk).
This is consistent with the often-heard guideline that we should limit the f-number to that which will give an Airy disk that is two pixel pitches in diameter (one pixel pitch in radius).
That is, that suggested limiting f-number is about 1.4 times the pixel pitch in µm.
This again seems to comport well with anecdotal reports of actual photographic reality.
I do not of course in any way mean to suggest the following that guideline in shot planning for any given photographic situation.
Best regards,
Doug
This discussion is gravely hampered by the facts that:
• There is no actual analytical definition of the "resolution" of a system.
• There is no obvious criterion of how much diminution of this elusive property is "unacceptable".
But let's see what we do know about the relationships involved.
The phenomenon of diffraction means that, assuming a perfect lens, a point on the object will be imaged not as a point but as a finite-sized "diffraction figure", which for a circular aperture with "knife edges" will have the illuminance pattern we call the "Airy figure". We can characterize this analytically as a "point spread function".
This spreading results in a decrease in the "response" of the system (a declining MTF) as the spatial frequency increases.
For any given point spread function, there is a unique MTF curve, which can be rigorously calculated by straightforward mathematics.
In the case of our ideal circular aperture, that MTF curve is as shown by the solid line on this figure:

The label "diffraction-limited MTF" (not mine, but that of the author of this curve) means that this would be the MTF of the entire system if diffraction was the overwhelming phenomenon; that is, if there were only diffraction to contend with. In other words, this is the MTF of the diffraction phenomenon.
Note that the MTF goes to zero at a spatial frequency of 1/LN, where N is the f-number of the aperture in use and L is the wavelength.I use "L" here rather than lambda, as on the figure, owing to possible character set problems.
We see that most of this curve can be well approximated by a straight line which goes to zero at a spatial frequency of 1/1.22LN.Recall that the MTF of the system is the MTF of the lens and the sensor multiplied (at each spatial frequency) by this MTF.
We often choose to say, quite arbitrarily, that the resultion of the entire system is the spatial frequency where the system MTF is 50%. Perhaps it is reasonable to say, equally arbitrarily, that the impact of diffraction on the resolution is "significant" at the spatial frequency where the diffraction MTF is 50%.
We see this on the chart as a spatial frequency of 1/2.44LN.
Let's pause to note that 2.44LN is in fact the diameter of the Airy disk (that is, the diameter of the Airy figure out to its first minimum).
Now, what might this actually mean in a real photographic situation?Let's say that we choose an f-number such that the zero of the straight line approximation of the diffraction MTF is at the Nyquist frequency of the sensor. Recall that this is an absolute limit on the spatial frequency that can be captured by the system (even with a "perfect" lens and negligible diffraction effect). That is, we have arranged for the response due to diffraction (in its straight line approximation) to just "poop out" at the Nyquist frequency, at or above which the sensor could not possible respond anyway.
The Nyquist frequency is defined as 1/2p, where p is the sensel pitch of the sensor. (We will assume a monochrome sensor to avert the need to deal with the complications of a CFA sensor, and assume a wavelength of 555 nm, as is common in this matter.)
After a little algebra, we find that in the situation where the diffraction MTF is 50%, the diameter of the Airy circle is twice the pixel pitch (or, the pixel pitch is the radius of the Airy disk).
This is consistent with the often-heard guideline that we should limit the f-number to that which will give an Airy disk that is two pixel pitches in diameter (one pixel pitch in radius).
That is, that suggested limiting f-number is about 1.4 times the pixel pitch in µm.
This again seems to comport well with anecdotal reports of actual photographic reality.
I do not of course in any way mean to suggest the following that guideline in shot planning for any given photographic situation.
Best regards,
Doug
