Fotis D. Tirokomos
New member
Dear community,
The study I would like to present here constitutes an original piece of work, devised and carried out by yours truly, as an attempt to answer certain questions related to the foundation of operation of hand held light (flash) meters.
This work is purely technical, involving some mathematical approach, just to be able to introduce and analyze the theoretical model adopted and to check if this model’s foreseen results are verified in reality, by taking actual measurements with a camera and a series of different lenses.
This work is definitely not to be perceived and not aimed as a “How to Use” a light (flash in this case) meter technical manual or a Tutorial on light meter handling, but it can be used, I believe, as a guide for testing out different lenses regarding their influence to the exposure determination. But certainly, it is not my aim to suggest that everybody should test every lens he or she can lay hands on, in order to be “accurate” in light metering, since “light metering is a serious and extremely complicated process, meant only for serious photographers” – NO! – I simply make an attempt to find out what are light meters specifically designed to do and why.
Dear Doug, as you are the Moderator here, please let me know if this is the right place for this study to be presented, or it is better to be somewhere else or nowhere at all, if this work does not interest this community!
The questions I am asking in specific are the following:
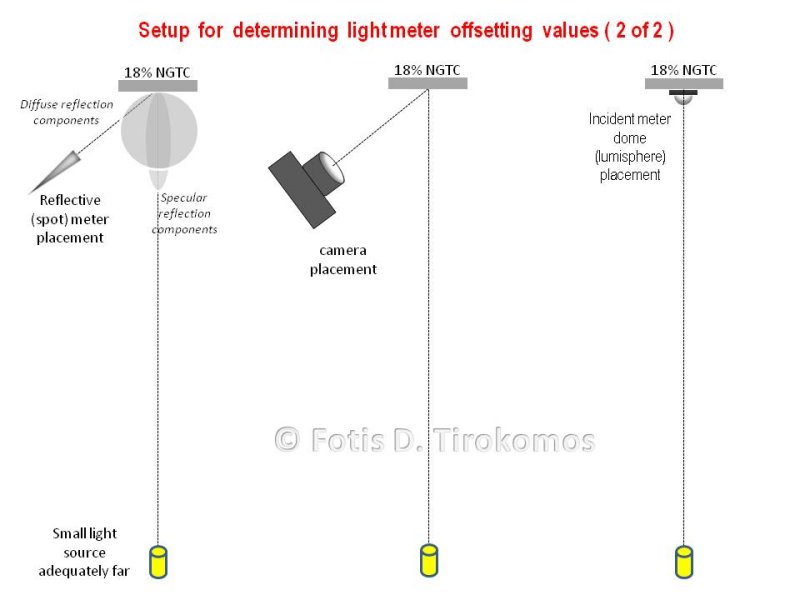
- Why do I usually get different readings between reflected and incident (dome open) light measurements, taken for the same 18% reference reflectance Neutral Grey Test Card (18% NGTC)?
- What kind or reference reflectance (11.55%, 12%, 12.5%, 12.7%, 15.7%, 18%, other?) is implied for the calibration of a Reflective Light (flash in this case) meter?
- In practice, what kind of offsetting would a lens introduce to a light meter measurement?
Before torturing the reader with the basis, argumentation and analysis of these points, let me outline my findings right away:
- A Light (Flash) Meter at Incident - dome open (‘lumisphere”) measuring mode is designed to better fit with the lighting conditions of a 3-D subject. When this mode is used for a 2-D subject like a 18% NGTC surface it is normal to generally suggest different readings from a reflected light measurement of the same 18%NGTC.
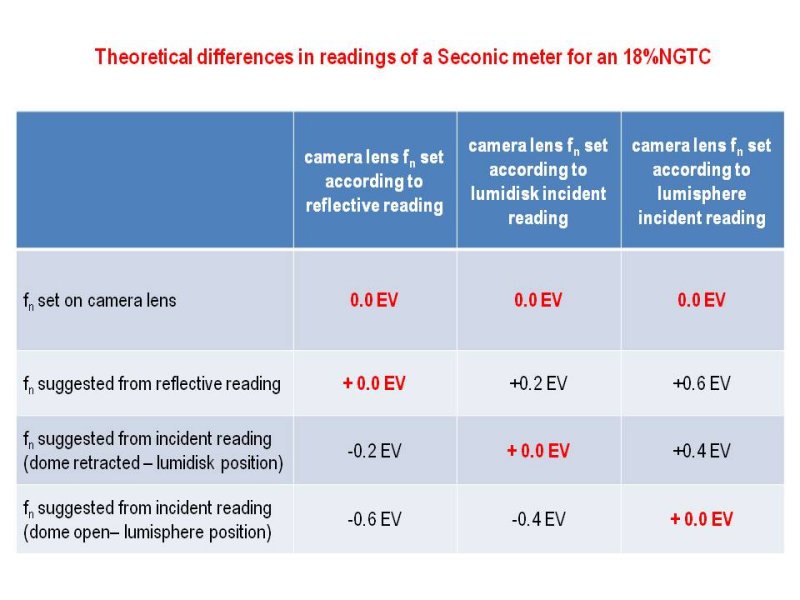
- Light (Flash) Meters in reflective metering mode as well as in incident - dome retracted (“lumidisk”) mode, are in line with the concept of 18% tonality reference, as expressed in the raw image color histogram of a spike at the center of it.
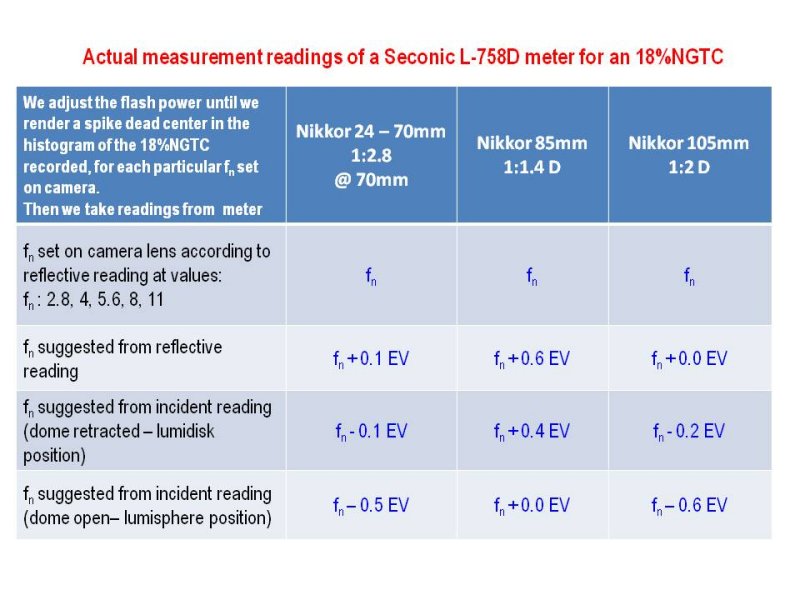
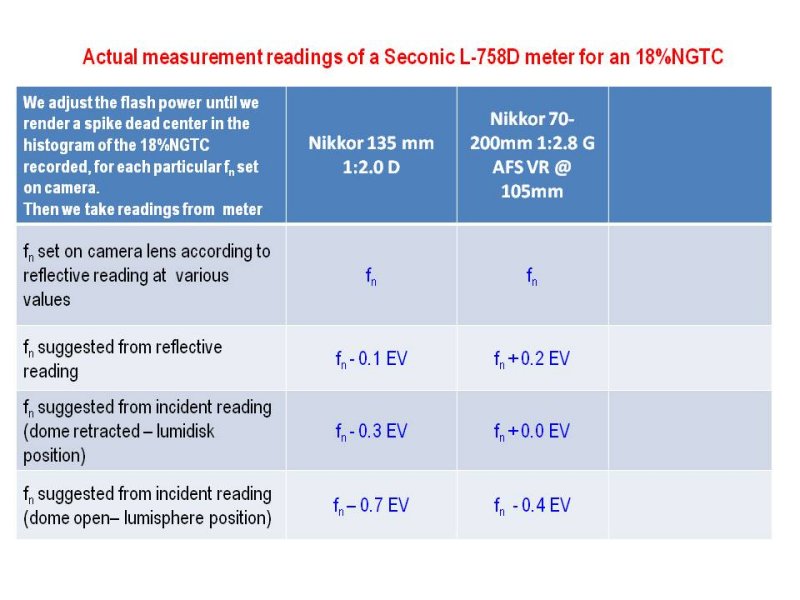
- If an offset is to be introduced so as to account for the influence of a particular camera – lens system used to the meter reading, this is to better to be done with reference to reflective and or incident – mode retracted (“lumidisk”) measuring modes – not to the incident – dome open (“lumisphere”) mode. Typical offsets are ranging within of 0.3 stop.
In the next part I shall proceed with the analysis to support what is just stated.
The study I would like to present here constitutes an original piece of work, devised and carried out by yours truly, as an attempt to answer certain questions related to the foundation of operation of hand held light (flash) meters.
This work is purely technical, involving some mathematical approach, just to be able to introduce and analyze the theoretical model adopted and to check if this model’s foreseen results are verified in reality, by taking actual measurements with a camera and a series of different lenses.
This work is definitely not to be perceived and not aimed as a “How to Use” a light (flash in this case) meter technical manual or a Tutorial on light meter handling, but it can be used, I believe, as a guide for testing out different lenses regarding their influence to the exposure determination. But certainly, it is not my aim to suggest that everybody should test every lens he or she can lay hands on, in order to be “accurate” in light metering, since “light metering is a serious and extremely complicated process, meant only for serious photographers” – NO! – I simply make an attempt to find out what are light meters specifically designed to do and why.
Dear Doug, as you are the Moderator here, please let me know if this is the right place for this study to be presented, or it is better to be somewhere else or nowhere at all, if this work does not interest this community!
The questions I am asking in specific are the following:
- Why do I usually get different readings between reflected and incident (dome open) light measurements, taken for the same 18% reference reflectance Neutral Grey Test Card (18% NGTC)?
- What kind or reference reflectance (11.55%, 12%, 12.5%, 12.7%, 15.7%, 18%, other?) is implied for the calibration of a Reflective Light (flash in this case) meter?
- In practice, what kind of offsetting would a lens introduce to a light meter measurement?
Before torturing the reader with the basis, argumentation and analysis of these points, let me outline my findings right away:
- A Light (Flash) Meter at Incident - dome open (‘lumisphere”) measuring mode is designed to better fit with the lighting conditions of a 3-D subject. When this mode is used for a 2-D subject like a 18% NGTC surface it is normal to generally suggest different readings from a reflected light measurement of the same 18%NGTC.
- Light (Flash) Meters in reflective metering mode as well as in incident - dome retracted (“lumidisk”) mode, are in line with the concept of 18% tonality reference, as expressed in the raw image color histogram of a spike at the center of it.
- If an offset is to be introduced so as to account for the influence of a particular camera – lens system used to the meter reading, this is to better to be done with reference to reflective and or incident – mode retracted (“lumidisk”) measuring modes – not to the incident – dome open (“lumisphere”) mode. Typical offsets are ranging within of 0.3 stop.
In the next part I shall proceed with the analysis to support what is just stated.