Doug Kerr
Well-known member
One class of color models (the bases for color spaces) describes color in terms of two aspects, luminance and chromaticity. Chromaticity requires two coordinates to describe it, which can be done in several ways. One way describes chromaticity in terms of the subordinate properties hue and saturation.
We can think of hue as the property that distinguishes red from blue, and saturation as the property that distinguishes red from pink.
But if we wanted to make saturation one of the coordinates of a specific color space, we have to do better than that. We have to adopt some quantitative definition of saturation, a way to give the saturation of some color a numerical value.
There is in fact no unique quantitative definition of saturation in formal colorimetry. (We'll get some hint later as to why that is.) Two definitions, however, can be useful.
Visible gamut based saturation
Here, we see the CIE x-y chromaticity diagram. Any point on its "x-y plane" represents a chromaticity. The region inside the "spectral horseshoe" (with its end closed by the "locus of purples") is the visible gamut. We show the sRGB primaries, R, G, and B, and the associated "low luminance chrominance gamut boundary" triangle, for reference, although they don't really figure into the scheme I'll be discussing in this section. We also see the sRGB white point chromaticity W, which does figure in.
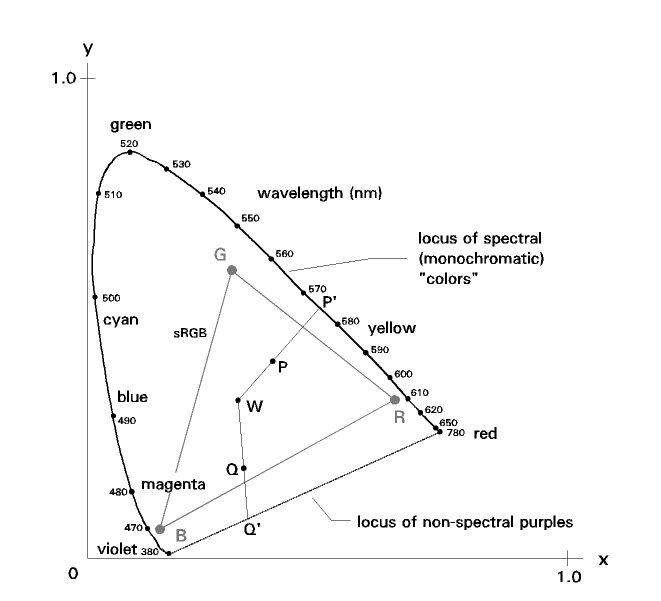
One useful definition of saturation is a quantity also called excitation purity. It is based on the concept that a "spectral" color whose hue is the same as the hue of the color of interest is considered "pure" and thus has a saturation of 1.0 (100%). White light (whatever we mean by that*) has a saturation of 0.
Thus, for color "P" (we only see its chromaticity here), which has a "spectral" hue, the saturation, S(P) is given by:
S(P)= (distance W-P)/(distance W-P')
For chromaticities whose hue is not spectral (that is, whose hue is that of a "non-spectral purple"), a similar principle applies. For example, for chromaticity "Q", the saturation, S(Q), is given by:
S(Q)= (distance W-Q)/(distance W-Q')
Note that this reckoning (both forms) is based on the use of the CIE x-y chromaticity diagram (1931). Were we to do this work on either the CIE u-v chromaticity diagram (1960) or the CIE u'v' chromaticity diagram (1976), we would, in general, get a different result (the same for those two, however!).
Thus, not only does the definition of saturation vary with the assumed white point (it must, since, for example, we consider "white" to have saturation=0) but also on the turf in which we make our reckoning.
It is no wonder that there is no CIE quantitative definition of "saturation".
RGB gamut based saturation
Another useful measure of saturation compares the chromaticity the color of interest with the chromaticity of the "highest saturation color of the same hue" that can be represented in the color space of interest. We can follow that concept on this figure:
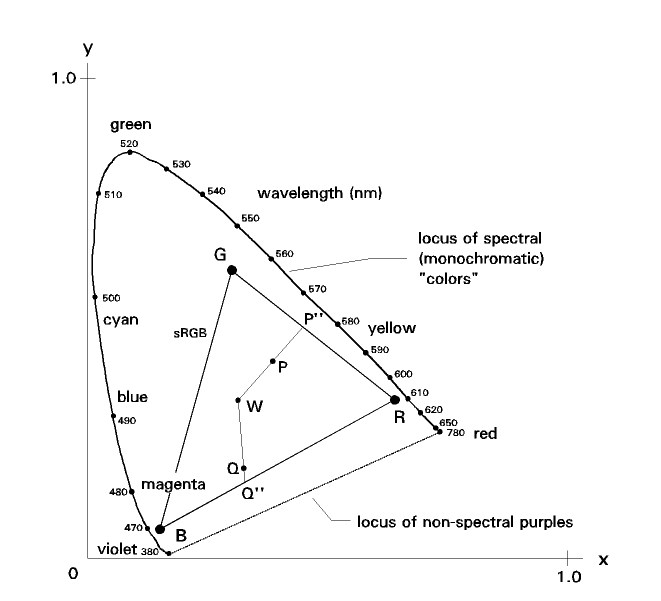
The highest saturation colors that can be represented in this color space (sRGB is illustrated) are those lying on the "low luminance chrominance gamut boundary", the triangle joining the chromaticities of the three primaries, R, G, and B. These are all colors for which at least one of R, G, or B is zero.
The basic concept is much the same as before. For color "P" (which has a "spectral" hue), the "RGB-based" saturation, s(P), is given by:
s(P)= (distance W-P)/(distance W-P'')
For color "Q" (which has a "non-spectral" hue), the "RGB-based" saturation, s(Q), is given by:
s(Q)= (distance W-Q)/(distance W-Q'')
Dependence on work space
Note that this reckoning (both forms) is based on the use of the CIE x-y chromaticity diagram (1931). Were we to do this work on either the CIE u-v chromaticity diagram (1960) or the CIE u'v' chromaticity diagram (1976), we would, in general, get a different result (the same for those two, however!).
Thus, not only does the definition of saturation vary with the assumed white point (this is to be expected, since, for example, we consider "white" to have saturation=0) but also on the turf in which we make our reckoning.
It is no wonder that there is no CIE quantitative definition of "saturation".
HSB, HSL, and HSV color models
In color models of this family, one of the coordinates is always labeled "S", which we tend to think of as mnemonic for "saturation". Indeed, this property is always something like saturation, but it never follows either of the definitions discussed above.
This matter is beyond the scope of this note.
Best regards,
Doug
We can think of hue as the property that distinguishes red from blue, and saturation as the property that distinguishes red from pink.
But if we wanted to make saturation one of the coordinates of a specific color space, we have to do better than that. We have to adopt some quantitative definition of saturation, a way to give the saturation of some color a numerical value.
There is in fact no unique quantitative definition of saturation in formal colorimetry. (We'll get some hint later as to why that is.) Two definitions, however, can be useful.
Visible gamut based saturation
Here, we see the CIE x-y chromaticity diagram. Any point on its "x-y plane" represents a chromaticity. The region inside the "spectral horseshoe" (with its end closed by the "locus of purples") is the visible gamut. We show the sRGB primaries, R, G, and B, and the associated "low luminance chrominance gamut boundary" triangle, for reference, although they don't really figure into the scheme I'll be discussing in this section. We also see the sRGB white point chromaticity W, which does figure in.

One useful definition of saturation is a quantity also called excitation purity. It is based on the concept that a "spectral" color whose hue is the same as the hue of the color of interest is considered "pure" and thus has a saturation of 1.0 (100%). White light (whatever we mean by that*) has a saturation of 0.
*And this means that the reckoning of saturation must be predicated on some assumed chromaticity of "white", perhaps the white point of some color space of interest.
Thus, for color "P" (we only see its chromaticity here), which has a "spectral" hue, the saturation, S(P) is given by:
S(P)= (distance W-P)/(distance W-P')
For chromaticities whose hue is not spectral (that is, whose hue is that of a "non-spectral purple"), a similar principle applies. For example, for chromaticity "Q", the saturation, S(Q), is given by:
S(Q)= (distance W-Q)/(distance W-Q')
Note that this reckoning (both forms) is based on the use of the CIE x-y chromaticity diagram (1931). Were we to do this work on either the CIE u-v chromaticity diagram (1960) or the CIE u'v' chromaticity diagram (1976), we would, in general, get a different result (the same for those two, however!).
Thus, not only does the definition of saturation vary with the assumed white point (it must, since, for example, we consider "white" to have saturation=0) but also on the turf in which we make our reckoning.
It is no wonder that there is no CIE quantitative definition of "saturation".
RGB gamut based saturation
Another useful measure of saturation compares the chromaticity the color of interest with the chromaticity of the "highest saturation color of the same hue" that can be represented in the color space of interest. We can follow that concept on this figure:

The highest saturation colors that can be represented in this color space (sRGB is illustrated) are those lying on the "low luminance chrominance gamut boundary", the triangle joining the chromaticities of the three primaries, R, G, and B. These are all colors for which at least one of R, G, or B is zero.
The basic concept is much the same as before. For color "P" (which has a "spectral" hue), the "RGB-based" saturation, s(P), is given by:
s(P)= (distance W-P)/(distance W-P'')
For color "Q" (which has a "non-spectral" hue), the "RGB-based" saturation, s(Q), is given by:
s(Q)= (distance W-Q)/(distance W-Q'')
Dependence on work space
Note that this reckoning (both forms) is based on the use of the CIE x-y chromaticity diagram (1931). Were we to do this work on either the CIE u-v chromaticity diagram (1960) or the CIE u'v' chromaticity diagram (1976), we would, in general, get a different result (the same for those two, however!).
Thus, not only does the definition of saturation vary with the assumed white point (this is to be expected, since, for example, we consider "white" to have saturation=0) but also on the turf in which we make our reckoning.
It is no wonder that there is no CIE quantitative definition of "saturation".
HSB, HSL, and HSV color models
In color models of this family, one of the coordinates is always labeled "S", which we tend to think of as mnemonic for "saturation". Indeed, this property is always something like saturation, but it never follows either of the definitions discussed above.
This matter is beyond the scope of this note.
Best regards,
Doug
