Doug Kerr
Well-known member
Especially in discussions of lighting technique, we often hear about the inverse square law.
I'll state it here in a quite precise form; I will used numbered notes to state important qualifications so as not to disturb the rhythm of the basic definition.
If we consider emission of light from a point source [1] in a particular direction [2], the luminous flux density of the "beam" varies as the inverse of the square of the distance from the source.
The variation in luminous flux density is also the variation in the illuminance deposited on a surface at that distance (for any given angle of arrival). In fact, it is this with which we are normally ultimately interested in matters of photographic exposure.
If we are thinking about a shoe-mounted flash unit, and subjects at substantial distances, the "point source" situation is fairly well followed.
But what happens if we do not have a point source - if we have what is called an "extended" source, one whose dimensions are not inconsequential, then the inverse square law does not pertain. This would typically be so for the usual studio or field lighting system.
The relationship of luminous flux density (and thus of illuminance) with distance is very complex in the general case. We can treat it handily if we assume a very ideal light source. Its properties are:
• Its face is circular
• Its luminance is uniform across its face.
• Its emission is Lambertian. One thing that means is that its luminance is the same regardless of from what angle the source is viewed.
Such a source is shown in this figure.
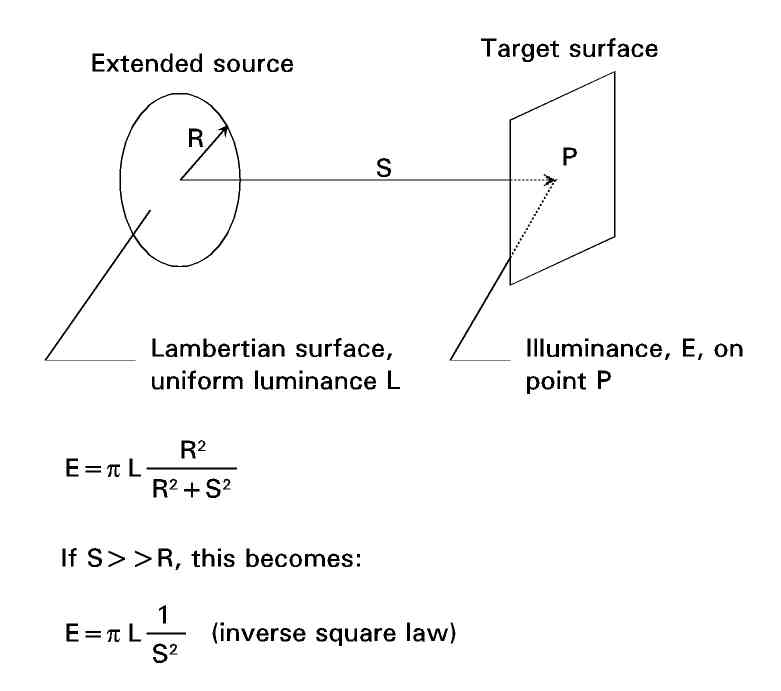
The source is circular, with radius R. Its luminance is L at every place on its face. Its emission is Lambertian.
We consider a subject surface at a distance of S from the source (measured along a line from the center of the source and perpendicular to it). The subject plane is parallel to the source (perpendicular to the aforementioned line). Our interest is in the illuminance, E, created by the source on a point, P, on the subject plane, on the aforementioned line.
The figure shows the mathematical expression for this illuminance. You will see that it does not correspond to the inverse square law (the relationship is more complicated than that).
But, if we envision a situation in which the distance is substantially greater than the radius of the source (that is, the size of the source is "negligible" compared to the distance to the subject - we can consider it be essentially a point source), the expression degenerates to a simpler one - exactly the inverse square law.
What happens if:
• The source face isn't circular?
• The luminance is not uniform across the source face?
• The emission from the source isn't Lambertian?
• The target point of interest is not on the perpendicular line from the center of the source?
For almost any actual situation of photographic interest, one or more of these would be so.
In such a case, the relationship would not be the simple one shown in the figure. Exactly what it would be would of course depend on the specific details of all the behavioral factors mentioned above.
Best regards,
Doug
I'll state it here in a quite precise form; I will used numbered notes to state important qualifications so as not to disturb the rhythm of the basic definition.
If we consider emission of light from a point source [1] in a particular direction [2], the luminous flux density of the "beam" varies as the inverse of the square of the distance from the source.
[1] A source whose dimensions are very small compared to the distance at which we consider its influence.
[2] A point source does not by definition necessarily exhibit the same luminous intensity in every direction.
[2] A point source does not by definition necessarily exhibit the same luminous intensity in every direction.
The variation in luminous flux density is also the variation in the illuminance deposited on a surface at that distance (for any given angle of arrival). In fact, it is this with which we are normally ultimately interested in matters of photographic exposure.
If we are thinking about a shoe-mounted flash unit, and subjects at substantial distances, the "point source" situation is fairly well followed.
But what happens if we do not have a point source - if we have what is called an "extended" source, one whose dimensions are not inconsequential, then the inverse square law does not pertain. This would typically be so for the usual studio or field lighting system.
The relationship of luminous flux density (and thus of illuminance) with distance is very complex in the general case. We can treat it handily if we assume a very ideal light source. Its properties are:
• Its face is circular
• Its luminance is uniform across its face.
• Its emission is Lambertian. One thing that means is that its luminance is the same regardless of from what angle the source is viewed.
Such a source is shown in this figure.

The source is circular, with radius R. Its luminance is L at every place on its face. Its emission is Lambertian.
We consider a subject surface at a distance of S from the source (measured along a line from the center of the source and perpendicular to it). The subject plane is parallel to the source (perpendicular to the aforementioned line). Our interest is in the illuminance, E, created by the source on a point, P, on the subject plane, on the aforementioned line.
The figure shows the mathematical expression for this illuminance. You will see that it does not correspond to the inverse square law (the relationship is more complicated than that).
But, if we envision a situation in which the distance is substantially greater than the radius of the source (that is, the size of the source is "negligible" compared to the distance to the subject - we can consider it be essentially a point source), the expression degenerates to a simpler one - exactly the inverse square law.
What happens if:
• The source face isn't circular?
• The luminance is not uniform across the source face?
• The emission from the source isn't Lambertian?
• The target point of interest is not on the perpendicular line from the center of the source?
For almost any actual situation of photographic interest, one or more of these would be so.
In such a case, the relationship would not be the simple one shown in the figure. Exactly what it would be would of course depend on the specific details of all the behavioral factors mentioned above.
Best regards,
Doug
