Doug Kerr
Well-known member
Especially in connection with white balance color correction, we often hear about color temperature. It seems as if that is a way to describe the chromaticity of an illuminant, and we need to know that to, for example, set up white balance color correction in postprocessing.
Now of course we really need to know more than the chromaticity of the illuminant to fully deal with the matter of white balance color correction, but that is a topic for another time.
But what about color temperature? What's that all about?
Well color temperature itself is a way to describe the chromaticity of light, but only when that chromaticity of a very limited class: the chromaticity of a blackbody radiation. What is that?
Well a black body (it is an editorial convention to spell "black body" as a noun in two words, but "blackbody" used as an adjective phrase as one word, and I follow that) is a surface that absorbs all the visible radiation that falls on it, at whatever visible wavelength. So it is no surprise that one of them would look "black", and thus its name.
But any object at a temperature of greater than absolute zero (0 K) radiates. The spectrum of its radiation depends on the temperature and the nature of the surface. For a black body, we know exactly its spectrum for any given temperature, and from that we can determine the chromaticity of that radiation (so long as part of it is in the visible range; otherwise the radiation would not be "light" and would not have a chromaticity).
We often use a CIE x-y diagram to graphically indicate chromaticity. Here:
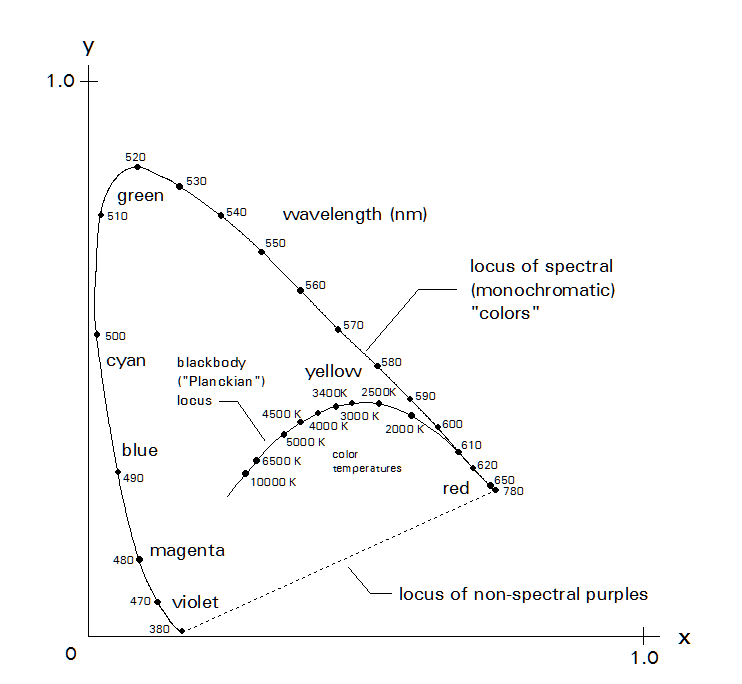
we see such a chart, showing the familiar horseshoe-shaped "locus of spectral colors" and "locus of non-spectral purples" that bound the region of visible light.
Also on this chart is plotted the chromaticity of a blackbody radiator for a range of its temperatures. Thus is called the "blackbody locus", or the "Planckian locus", the latter name honoring noted physicist Max Planck, who did much of the work to determine the theoretical behavior of a blackbody radiator.
This is basically that same chart:
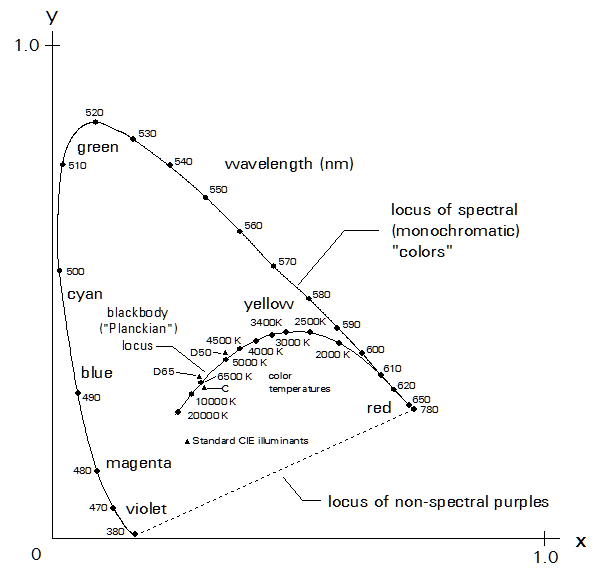
but I have shown on it the chromaticities of some standard illuminants we often speak of, such as "Illuminant D65". We see that the various "daylight" illuminants do not have chromaticities very far from the Planckian locus, not too surprising because the sun is very similar to a black body in this respect.
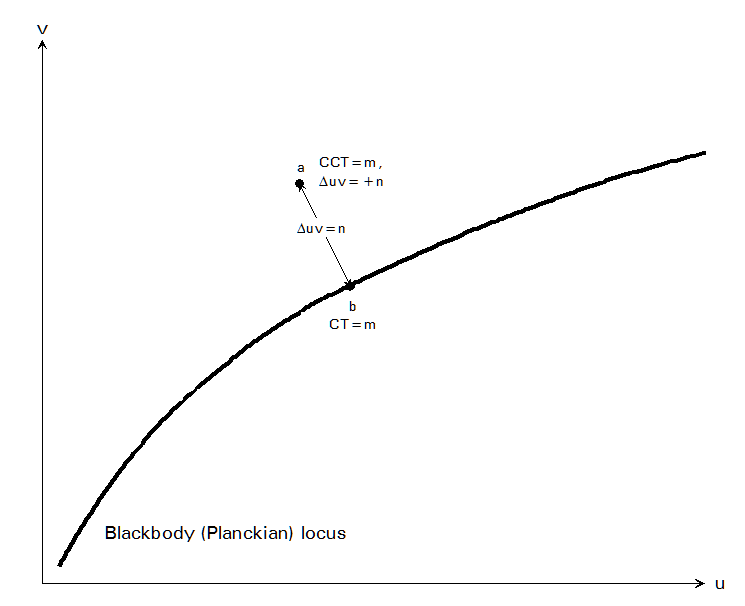
Now for any chromaticity of light that lies on the Planckian locus, we can describe that chromaticity just by mentioning the temperature of a black body whose radiation would have that chromaticity. And that is of course known as the color temperature of that radiation.
Now what about a chromaticity that does not fall on the Planckian locus? What is its color temperature? Well, it doesn't have one. Only the chromaticities on the Planckian locus can be described in terms of their color temperature.
But we can extend the concept of color temperature to cover chromaticities not on the Planckian locus (although this is not really desirable for chromaticities that are very far from the Planckian locus). What we do is determine the point on the Planckian locus that is "nearest to" the point for the chromatically of interest. Then, the color temperature of that point on the Planckian locus is said to be the correlated color temperature (CCT) of the chromaticity of interest. We see that on this figure:

We see several chromaticity points which, because they are "nearest" the point on the Planckian locus with color temperature 5000 K are said to have correlated color temperatures of 5000 K. And in fact there is a while line every point on which has a CCT of 5000 K.
But actually, that figure is not accurate. The issue is what do we mean the "nearest" point on the Planckian locus? Well, by that we mean the point on the Planckian locus whose distance from the point of interest is the least possible. And the line I spoke of in this figure follows that. But there is a clinker.
The CIE x-y chromaticity diagram is the one most familiar to us, and it was the first one devised, attractive since x and y are derived very simply from the underlying coordinates of a color, X, Y, and Z. But is less desirable in that distances on this chart doe not track well with the degree of perceived difference in chromaticity on the part of a human observer.
There is another CIE chromaticity diagram that improves on that matter. Its coordinates are called (just to distinguish them from x and y) u and v.
And in fact, the determination of "what point on the Planckian locus is nearest the point for the chromaticity we are trying to describe" is done on the CIE u-v chromaticity diagram. We can see that here:
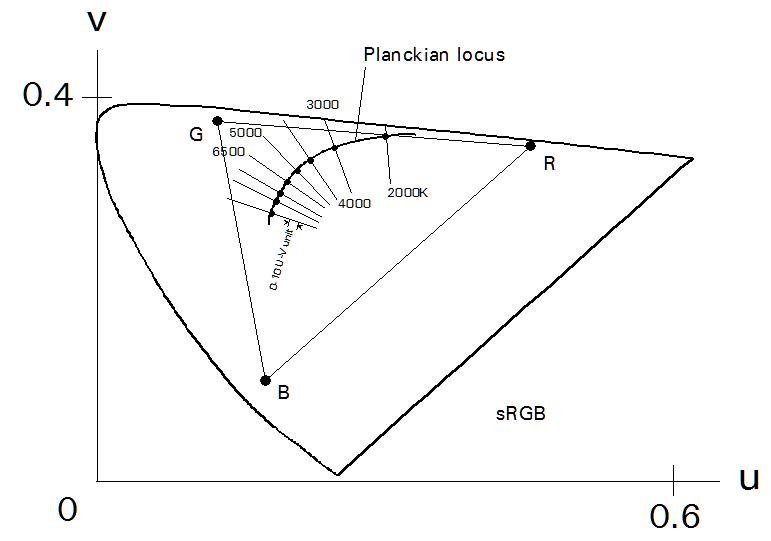
We see here the Planckian locus and the lines consisting of points that are "nearest" points on the Planckian locus with various color temperatures. So any chromaticity whose point lies on the line labeled "5000 K" has a correlated color temperature of 5000 K.
[continued]
Now of course we really need to know more than the chromaticity of the illuminant to fully deal with the matter of white balance color correction, but that is a topic for another time.
But what about color temperature? What's that all about?
Well color temperature itself is a way to describe the chromaticity of light, but only when that chromaticity of a very limited class: the chromaticity of a blackbody radiation. What is that?
Well a black body (it is an editorial convention to spell "black body" as a noun in two words, but "blackbody" used as an adjective phrase as one word, and I follow that) is a surface that absorbs all the visible radiation that falls on it, at whatever visible wavelength. So it is no surprise that one of them would look "black", and thus its name.
But any object at a temperature of greater than absolute zero (0 K) radiates. The spectrum of its radiation depends on the temperature and the nature of the surface. For a black body, we know exactly its spectrum for any given temperature, and from that we can determine the chromaticity of that radiation (so long as part of it is in the visible range; otherwise the radiation would not be "light" and would not have a chromaticity).
We often use a CIE x-y diagram to graphically indicate chromaticity. Here:

we see such a chart, showing the familiar horseshoe-shaped "locus of spectral colors" and "locus of non-spectral purples" that bound the region of visible light.
Also on this chart is plotted the chromaticity of a blackbody radiator for a range of its temperatures. Thus is called the "blackbody locus", or the "Planckian locus", the latter name honoring noted physicist Max Planck, who did much of the work to determine the theoretical behavior of a blackbody radiator.
This is basically that same chart:

but I have shown on it the chromaticities of some standard illuminants we often speak of, such as "Illuminant D65". We see that the various "daylight" illuminants do not have chromaticities very far from the Planckian locus, not too surprising because the sun is very similar to a black body in this respect.
Now for any chromaticity of light that lies on the Planckian locus, we can describe that chromaticity just by mentioning the temperature of a black body whose radiation would have that chromaticity. And that is of course known as the color temperature of that radiation.
Now what about a chromaticity that does not fall on the Planckian locus? What is its color temperature? Well, it doesn't have one. Only the chromaticities on the Planckian locus can be described in terms of their color temperature.
But we can extend the concept of color temperature to cover chromaticities not on the Planckian locus (although this is not really desirable for chromaticities that are very far from the Planckian locus). What we do is determine the point on the Planckian locus that is "nearest to" the point for the chromatically of interest. Then, the color temperature of that point on the Planckian locus is said to be the correlated color temperature (CCT) of the chromaticity of interest. We see that on this figure:

We see several chromaticity points which, because they are "nearest" the point on the Planckian locus with color temperature 5000 K are said to have correlated color temperatures of 5000 K. And in fact there is a while line every point on which has a CCT of 5000 K.
But actually, that figure is not accurate. The issue is what do we mean the "nearest" point on the Planckian locus? Well, by that we mean the point on the Planckian locus whose distance from the point of interest is the least possible. And the line I spoke of in this figure follows that. But there is a clinker.
The CIE x-y chromaticity diagram is the one most familiar to us, and it was the first one devised, attractive since x and y are derived very simply from the underlying coordinates of a color, X, Y, and Z. But is less desirable in that distances on this chart doe not track well with the degree of perceived difference in chromaticity on the part of a human observer.
There is another CIE chromaticity diagram that improves on that matter. Its coordinates are called (just to distinguish them from x and y) u and v.
And in fact, the determination of "what point on the Planckian locus is nearest the point for the chromaticity we are trying to describe" is done on the CIE u-v chromaticity diagram. We can see that here:

We see here the Planckian locus and the lines consisting of points that are "nearest" points on the Planckian locus with various color temperatures. So any chromaticity whose point lies on the line labeled "5000 K" has a correlated color temperature of 5000 K.
[continued]
Last edited: