Doug Kerr
Well-known member
In connection with the matter of the conversion of color coordinates from linear to nonlinear form (as in the process sometimes called "gamma precompensation), we often hear the relationship described as an "exponential function".
It is not. It is a power function, a quite different thing.
Both kinds of function involve an exponent, which probably is one cause of the confusion. (I ran into the same thing once with regard to Mexico and New Mexico.)
Here we see in generalized form a power function (y as a function of x):
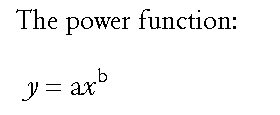
The constants a and b define the specific function.
Here we see in generalized form an exponential function (y as a function of x):
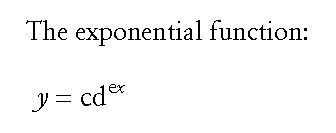
The constants c, d, and e define the specific function.
You can see that it entirely different from the power function. If we plot curves for both (perhaps for the "degenerate" cases, with all constants at 1), we will see that the relationships are quite different.
We can actually use any value we wish for d if we make the appropriate adjustment to e. (Mathematicians often prefer to use for d the Naperian base, often symbolized as e.)
If, with the power function, we have y and want to reconstruct x, we can use the inverse form of the function. Here we see that, with the function itself repeated for comparison. Two equivalent forms are shown.
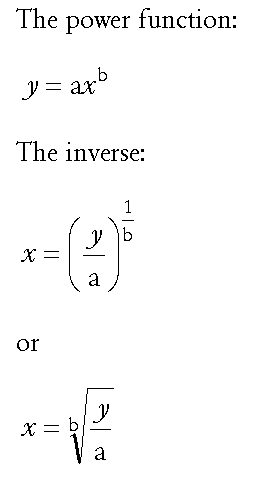
If, with the exponential function, we have y and want to reconstruct x, we can use the inverse form of the function, which is in fact the logarithmic function. Here we see that, with the function itself repeated for comparison.

It is not. It is a power function, a quite different thing.
Both kinds of function involve an exponent, which probably is one cause of the confusion. (I ran into the same thing once with regard to Mexico and New Mexico.)
Here we see in generalized form a power function (y as a function of x):
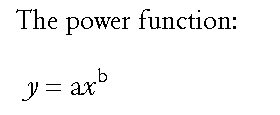
The constants a and b define the specific function.
Here we see in generalized form an exponential function (y as a function of x):
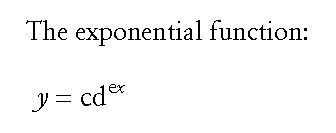
The constants c, d, and e define the specific function.
You can see that it entirely different from the power function. If we plot curves for both (perhaps for the "degenerate" cases, with all constants at 1), we will see that the relationships are quite different.
We can actually use any value we wish for d if we make the appropriate adjustment to e. (Mathematicians often prefer to use for d the Naperian base, often symbolized as e.)
If, with the power function, we have y and want to reconstruct x, we can use the inverse form of the function. Here we see that, with the function itself repeated for comparison. Two equivalent forms are shown.
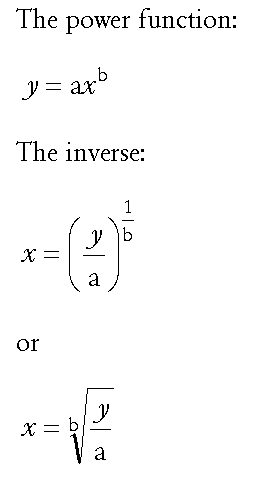
If, with the exponential function, we have y and want to reconstruct x, we can use the inverse form of the function, which is in fact the logarithmic function. Here we see that, with the function itself repeated for comparison.

