Doug Kerr
Well-known member
Two of the classical aberrations of a lens are called spherical aberration and coma. They are closely related.
Spherical aberration
Spherical aberration results from the fact that in a lens with a spherical surface (or two spherical surfaces), the rays from a point on the object that pass through the lens at different distances from its center (we often speak of them as passing through separate "zones" of the lens, where a "zone" is a ring-shaped region of the lens, usually considered infinitesimal in radial thickness) do not converge at a single point (as we would wish).
We see that here:
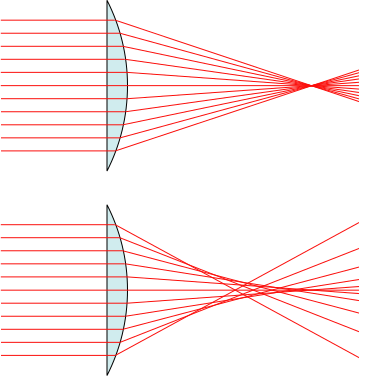
The upper panel shows what we would like (this lens presumably does not have a spherical surface). The lower panel shows the result of spherical aberration (this lens presumably does have a spherical surface).
If we place film, ground glass or a sensor at some point in image space (not shown on the figure - use your imagination), the "hollow cones" of rays passing through the different zones of the lens lay down individual rings of light (of infinitesimal radial thickness) on the film, except perhaps for one, which lays down a point. (Which one that is depends on exactly where we place the film.) These rings are all concentric.
Formally, spherical aberration is defined as an aberration affecting the imaging of an on-axis point. We will see why shortly.
Coma, spherical aberration's evil twin
Now again consider a practical lens with spherical surface(s), but consider an off-axis object point.
Here is an example:
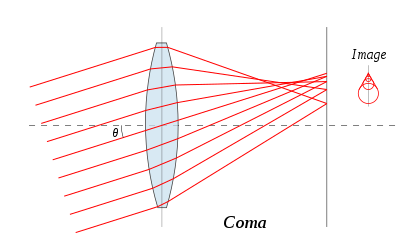
From Wikimedia Commons
Again, if we place film at a certain location (suggested by this figure) each of the "hollow cones" will deposit on the film a ring of light of infinitesimal radial thickness. The overall result will be a "comet-like" blur figure (thus the name of the aberration, coma).
In reality, we typically have two different aspects of the aberration:
• The rays through the different zones of the lens come to a focus at different distances from the lens (as we saw before). [Not as the figure shows!]
• The rays through the different zones of the lens have different transverse magnification, so the axes of their hollow cones make different angles with the axis, and the circles of light they deposit are at different distances from the axis.
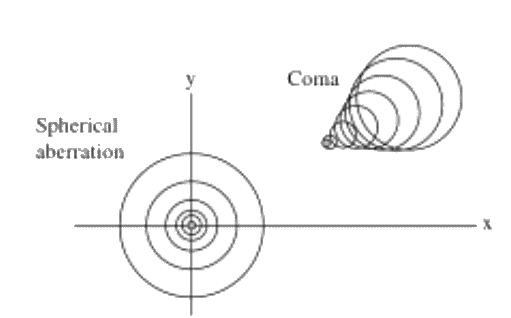
From Smith, F. Graham et al, Optics and Photonics: An Introduction, figure 2.27
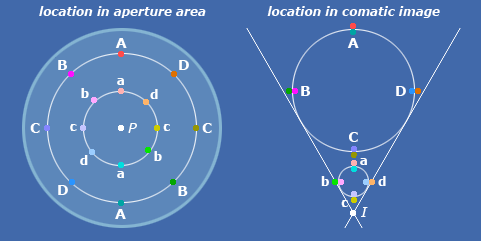
On the left ("spherical aberration"), we see six illustrative circles created on the focal plane by the hollow cones of rays from six zones (of infinitesimal radial thickness) on the lens.
On the right ("coma"), we see eight illustrative circles created on the focal plane by the hollow cones of rays from eight zones (of infinitesimal radial thickness) on the lens.
The semantics
So, isn't coma just the manifestation of the general case of spherical aberration for off-axis object points? Yes. But it is not the custom to say that. Rather, it is the custom to call it "coma".
Or perhaps spherical aberration is just a special case of coma, for an on-axis object point - where the discrepancy in lateral magnification for rays through different zones of the lens probably occurs but has no effect on the result.
Sure. But it is not the custom to say that. Rather, it is the custom to call it "spherical aberration".
Spherical aberration worse off-axis
We sometime hear that the impact of spherical aberration is worse for off-axis object points than fir on-axis points.
Almost certainly this usually refers to the phenomenon that is formally called "coma". And we would certainly expect the blur figure resulting from coma to have a larger envelope that that of the blur figure for (on-axis) spherical aberration.
But in fact some authors point out (as I did above) that this phenomenon comprises two aspects:
• The rays through the different zones of the lens come to a focus at different distances from the lens. They often refer to this as the "spherical aberration" aspect of coma.
• The rays through the different zones of the lens have different transverse magnification. They often refer to this as the "inconsistent lateral magnification" (or some such) aspect of coma.
Now, is the former of those two components, by itself, typically "greater" for off-axis points than for on-axis points? I don't know.
Addendum
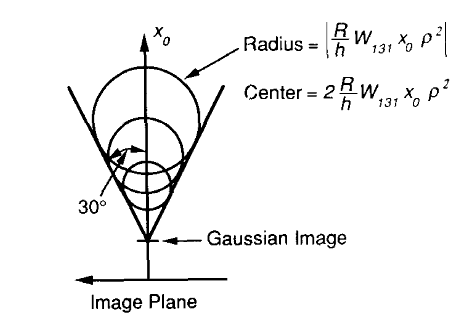
This figure shows coma without correction of spherical aberration, which does result in the "teardrop" shaped blur figure, but it's not easy to follow. I will try to adapt it in a later version of this note.
from Wikemedia Commons
Best regards,
Doug
Spherical aberration
Spherical aberration results from the fact that in a lens with a spherical surface (or two spherical surfaces), the rays from a point on the object that pass through the lens at different distances from its center (we often speak of them as passing through separate "zones" of the lens, where a "zone" is a ring-shaped region of the lens, usually considered infinitesimal in radial thickness) do not converge at a single point (as we would wish).
We see that here:

The upper panel shows what we would like (this lens presumably does not have a spherical surface). The lower panel shows the result of spherical aberration (this lens presumably does have a spherical surface).
If we place film, ground glass or a sensor at some point in image space (not shown on the figure - use your imagination), the "hollow cones" of rays passing through the different zones of the lens lay down individual rings of light (of infinitesimal radial thickness) on the film, except perhaps for one, which lays down a point. (Which one that is depends on exactly where we place the film.) These rings are all concentric.
Formally, spherical aberration is defined as an aberration affecting the imaging of an on-axis point. We will see why shortly.
Coma, spherical aberration's evil twin
Now again consider a practical lens with spherical surface(s), but consider an off-axis object point.
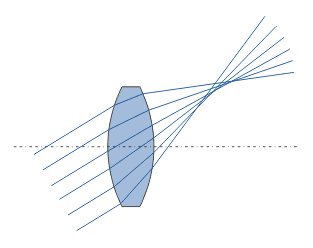
Here is an example:

From Wikimedia Commons
[There is a flaw in this figure which I will discuss in a moment; I'll look for a better one.]
Again, if we place film at a certain location (suggested by this figure) each of the "hollow cones" will deposit on the film a ring of light of infinitesimal radial thickness. The overall result will be a "comet-like" blur figure (thus the name of the aberration, coma).
The main portion of the figure suggests that all the hollow cones come to a focus on the film plane, as if spherical aberration itself has been corrected, perhaps by the use of a non-spherical lens. That is perfectly possible, but not likely. But that is in any case not consistent with the illustration of the resulting blur figure to the right. (That blur figure would be a line.)
In reality, we typically have two different aspects of the aberration:
• The rays through the different zones of the lens come to a focus at different distances from the lens (as we saw before). [Not as the figure shows!]
• The rays through the different zones of the lens have different transverse magnification, so the axes of their hollow cones make different angles with the axis, and the circles of light they deposit are at different distances from the axis.
This latter is actually true for a point on the axis, but we do not see it, since the axes of the hollow cones are all at zero distance from the axis; it doesn't matter if one of them is 1.1 times are far from the axis as another - they both are at zero distance.
We can see the distinction between the two situations here:
From Smith, F. Graham et al, Optics and Photonics: An Introduction, figure 2.27
On the left ("spherical aberration"), we see six illustrative circles created on the focal plane by the hollow cones of rays from six zones (of infinitesimal radial thickness) on the lens.
On the right ("coma"), we see eight illustrative circles created on the focal plane by the hollow cones of rays from eight zones (of infinitesimal radial thickness) on the lens.
The semantics
So, isn't coma just the manifestation of the general case of spherical aberration for off-axis object points? Yes. But it is not the custom to say that. Rather, it is the custom to call it "coma".
Or perhaps spherical aberration is just a special case of coma, for an on-axis object point - where the discrepancy in lateral magnification for rays through different zones of the lens probably occurs but has no effect on the result.
Sure. But it is not the custom to say that. Rather, it is the custom to call it "spherical aberration".
Spherical aberration worse off-axis
We sometime hear that the impact of spherical aberration is worse for off-axis object points than fir on-axis points.
Almost certainly this usually refers to the phenomenon that is formally called "coma". And we would certainly expect the blur figure resulting from coma to have a larger envelope that that of the blur figure for (on-axis) spherical aberration.
But in fact some authors point out (as I did above) that this phenomenon comprises two aspects:
• The rays through the different zones of the lens come to a focus at different distances from the lens. They often refer to this as the "spherical aberration" aspect of coma.
• The rays through the different zones of the lens have different transverse magnification. They often refer to this as the "inconsistent lateral magnification" (or some such) aspect of coma.
Now, is the former of those two components, by itself, typically "greater" for off-axis points than for on-axis points? I don't know.
Addendum
This figure shows coma without correction of spherical aberration, which does result in the "teardrop" shaped blur figure, but it's not easy to follow. I will try to adapt it in a later version of this note.

from Wikemedia Commons
Best regards,
Doug